ECCOv4 Global Volume Budget Closure¶
Here we demonstrate the closure of volume budgets in ECCOv4 configurations. This notebook is draws heavily from evaluating_budgets_in_eccov4r3.pdf which explains the procedure with Matlab code examples by Christopher G. Piecuch. See ECCO Version 4 release documents: /doc/evaluating_budgets_in_eccov4r3.pdf).
Objectives¶
Illustrate how volume budgets are closed globally.
Introduction¶
ECCOv4 uses the 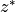 coordinate system in which the depth of the vertical coordinate,
coordinate system in which the depth of the vertical coordinate, 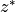 varies with time as:
varies with time as:
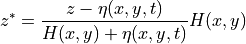
With  being the model depth,
being the model depth,  being the model sea level anomaly, and
being the model sea level anomaly, and  being depth.
being depth.
If the vertical coordinate didn’t change through time then volume fluxes across the ‘u’ and ‘v’ grid cell faces of a tracer cell could be calculated by multiplying the velocities at the face with the face area:
volume flux across ‘u’ face in the +x direction = 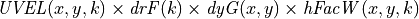
volume flux across ‘v’ face in the +y direction = 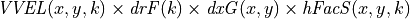
With dyG and dxG being the lengths of the ‘u’ and ‘v’ faces, drF being the grid cell height and hFacW and hFacS being the vertical fractions of the ‘u’ and ‘v’ grid cell faces that are open water (ECCOv4 uses partial cells to better represent bathymetry which can allows 0 < hfac  1).
1).
However, because the vertical coordiate varies with time in the  system, the grid cell height
system, the grid cell height drF varies with time as drF , with
, with
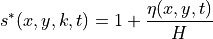
with 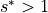 when
when 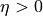
Thus, to calculate the volume fluxes grid cell through horizontal faces we must account for the time-varying grid cell face areas:
volume flux across ‘u’ in the +x direction face with 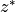 coordinates =
coordinates = 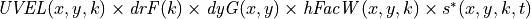
volume flux across ‘v’ in the +y direction face with 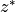 coordinates =
coordinates = 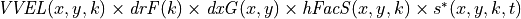
To make budget calculations easier we provide the scaled velocities quantities UVELMASS and VVELMASS,
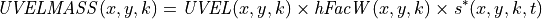
and
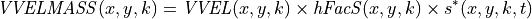
It is worth noting that the word mass in UVELMASS and VVELMASS is confusing since there is no mass involved here. Think of these terms as simply being UVEL and VVEL multiplied by the fraction of the grid cell height that is open grid cell face across which the volume transport occurs. Partial cell bathymetry can make this fraction (hFacW, hFacS) less than one, and the 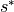 scaling factor further adjusts this fraction higher or lower through time.
scaling factor further adjusts this fraction higher or lower through time.
Fully closing the budget requires the vertical volume fluxes across the top and bottom ‘w’ faces of the grid cell and surface freshwater fluxes. Regarding vertical volume fluxes, there are no 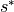 or
or hFac equivalent scaling factors that modify our top and bottom grid cell areas. Therefore, vertical volume fluxes through ‘w’ faces are simply:
volume flux across ‘w’ face in the +z direction = 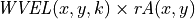
Note: Inexplicably, the term
WVELis provided with the silly nameWVELMASS. Sometimes it’s difficult to ignore other people’s poor life choices, but please try to do so here. Ignore the confusing name,WVELMASSis identical toWVEL.
In the 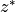 coordinate system the depth of the surface grid cell is always
coordinate system the depth of the surface grid cell is always 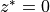 . In the MITgcm,
. In the MITgcm, WELMASS at the top of the surface grid cell is the liquid volume flux out of the ocean surface and is proportional to the vertical ocean mass flux, oceFWflx
ETAN in a Boussinesq Model¶
ECCOv4 uses a volume-conserving Boussinesq formulation of the MITgcm. Because volume is conserved in Boussinesq formulations, seawater density changes do not change model sea level anomaly, ETAN. The following demonstration ofETAN budget closure considers volumetric fluxes but does not take into consideration expansion/contraction due to changes in density. Furthermore, model ETAN changes with the exchange of water between ocean and sea-ice while in reality the Archimedes principle
holds that sea level should not change following the growth or melting of sea-ice because floating sea-ice displaces a volume of seawater equal to its weight. Thus, ETAN is not comparable to observed sea level.
We correct ETAN to make a sea surface height field that is comaprable with observations by making three corrections: with a) the “Greatbatch correction”, a time varying, globally-uniform correction to ocean volume due to changes in global mean density, b) the inverted barometer (IB) correction (see SSHIBC) and c) the ‘sea ice load’ correction to account for the displacement of seawater due to submerged sea-ice and snow (see sIceLoad). A demonstration of these corrections is outside
the scope of this tutorial. Here we focus on closing the model budget keeping in mind that we are neglecting sea level changes from changes in global mean density and the fact that ETAN does not account for volume displacement due to submerged sea-ice.
Greatbatch, 1994. J. of Geophys. Res. Oceans, https://doi.org/10.1029/94JC00847
Evaluating the model sea level anomaly ETAN volume budget¶
We will evalute
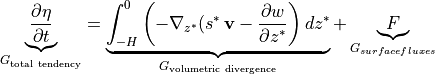
The total tendency of  ,
, 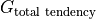 is the sum of the
is the sum of the  tendencies from volumetric divergence,
tendencies from volumetric divergence, 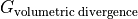 , and volumetric surface fluxes,
, and volumetric surface fluxes, 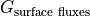 .
.
In discrete form, using indexes that start from k=0 (surface tracer cell) and running to k=nk-1 (bottom tracer cell)
![\frac{\eta(i,j)}{\partial t} = \sum_{k=nk-1}^{0} \underbrace{\left[\mathit{UVELMASS}(i_g,j,k)-\mathit{UVELMASS}(i_g+1,j,k) \right]\, \mathit{dyG}(i_g,j) \, \mathit{drF}(k) }_{\text{volumetric flux in minus out in x direction}} +
\\
\sum_{k=nk-1}^{0} \underbrace{\left[\mathit{VVELMASS}(i,j_g,k)-\mathit{VVELMASS}(i,j_g+1,k) \right] \, \mathit{dxG}(i,j_g) \, \mathit{drF}(k)}_{\text{volumetric flux in minus out in y direction}} +
\\
\sum_{k_l=nk}^{1} \underbrace{\mathit{WVELMASS}(i,j,k_l)\, \mathit{drA}(i,j)}_{\text{volumetric flux through grid cell bottom surface}} +
\\
\underbrace{\mathit{oceFWflx}(i,j)/ \mathit{rhoConst}}_{\text{volumetric flux through the top surface of the uppermost tracer cell}}](_images/math/b2d1c6b48fe183e4479d07cc656d8e6a56e93b72.png)
In the above we intentionally sum WVELMASS fluxes from the BOTTOM surface of the lowermost grid cell (at 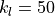 ) to the BOTTOM face of the uppermost grid cell (
) to the BOTTOM face of the uppermost grid cell (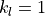 ) so that we can explicitly include the surface volume flux (forcing) term,
) so that we can explicitly include the surface volume flux (forcing) term, 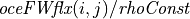 .
.
We will calculate 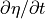 by differencing instantaneous monthly snapshots of
by differencing instantaneous monthly snapshots of  as
as
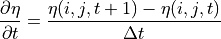
The UVELMASS, VVELMASS, WVELMASS and oceFWflx terms must be time-average quantities between the monthly  snapshots.
snapshots.
Datasets to download¶
If you don’t have any of the following datasets already, you will need to download them to complete the tutorial. Aside from the grid geometry file (which has no time dimension), you will need 2 monthly mean datasets for the full time span of ECCOv4r4 output (1992 through 2017), and 2 sets of snapshots at monthly intervals. The ShortNames of the datasets are:
ECCO_L4_GEOMETRY_LLC0090GRID_V4R4
ECCO_L4_OCEAN_3D_VOLUME_FLUX_LLC0090GRID_MONTHLY_V4R4 (1993-2016)
ECCO_L4_FRESH_FLUX_LLC0090GRID_MONTHLY_V4R4 (1993-2016)
ECCO_L4_SSH_LLC0090GRID_SNAPSHOT_V4R4 (1993/1/1-2017/1/1, 1st of each month)
ECCO_L4_OBP_LLC0090GRID_SNAPSHOT_V4R4 (1993/1/1-2017/1/1, 1st of each month)
If you haven’t yet been through the download tutorial or used the ecco_download module, it may help you to review that information before downloading the datasets. If you are downloading the snapshots, you may also find the
snaps_monthly_textlist function helpful; it generates a file list of only the snapshot files for the 1st of each month, which you can then download using wget.
Prepare environment and loading the relevant model variables¶
[1]:
import numpy as np
import sys
import xarray as xr
import glob
from copy import deepcopy
import matplotlib.pyplot as plt
%matplotlib inline
import warnings
warnings.filterwarnings('ignore')
[2]:
# setting up a dask LocalCluster
from dask.distributed import Client
from dask.distributed import LocalCluster
cluster = LocalCluster()
client = Client(cluster)
client
[2]:
Client
Client-f39e228e-ed5c-11ed-b1e0-c4236006c92f
| Connection method: Cluster object | Cluster type: distributed.LocalCluster |
| Dashboard: http://127.0.0.1:8787/status |
Cluster Info
LocalCluster
6de1e2d2
| Dashboard: http://127.0.0.1:8787/status | Workers: 4 |
| Total threads: 16 | Total memory: 31.78 GiB |
| Status: running | Using processes: True |
Scheduler Info
Scheduler
Scheduler-044a2a1a-db28-43f5-828c-ce440c4fd095
| Comm: tcp://127.0.0.1:50377 | Workers: 4 |
| Dashboard: http://127.0.0.1:8787/status | Total threads: 16 |
| Started: Just now | Total memory: 31.78 GiB |
Workers
Worker: 0
| Comm: tcp://127.0.0.1:50409 | Total threads: 4 |
| Dashboard: http://127.0.0.1:50410/status | Memory: 7.94 GiB |
| Nanny: tcp://127.0.0.1:50383 | |
| Local directory: C:\Users\adelman\AppData\Local\Temp\dask-worker-space\worker-ts5ue_66 | |
Worker: 1
| Comm: tcp://127.0.0.1:50415 | Total threads: 4 |
| Dashboard: http://127.0.0.1:50416/status | Memory: 7.94 GiB |
| Nanny: tcp://127.0.0.1:50381 | |
| Local directory: C:\Users\adelman\AppData\Local\Temp\dask-worker-space\worker-y2u9bou3 | |
Worker: 2
| Comm: tcp://127.0.0.1:50412 | Total threads: 4 |
| Dashboard: http://127.0.0.1:50413/status | Memory: 7.94 GiB |
| Nanny: tcp://127.0.0.1:50382 | |
| Local directory: C:\Users\adelman\AppData\Local\Temp\dask-worker-space\worker-yh7n3v78 | |
Worker: 3
| Comm: tcp://127.0.0.1:50418 | Total threads: 4 |
| Dashboard: http://127.0.0.1:50419/status | Memory: 7.94 GiB |
| Nanny: tcp://127.0.0.1:50380 | |
| Local directory: C:\Users\adelman\AppData\Local\Temp\dask-worker-space\worker-6h_ogg8v | |
[3]:
# Density kg/m^3
rhoconst = 1029
## needed to convert surface mass fluxes to volume fluxes
# lat/lon resolution in degrees to interpolate the model
# fields for the purposes of plotting
map_dx = .2
map_dy = .2
[4]:
## Import the ecco_v4_py library into Python
## =========================================
## If ecco_v4_py is not installed in your local Python library,
## tell Python where to find it. The example below adds
## ecco_v4_py to the user's path if it is stored in the folder
## ECCOv4-py under the user's home directory
from os.path import join,expanduser,exists,split
user_home_dir = expanduser('~')
sys.path.append(join(user_home_dir,'ECCOv4-py'))
import ecco_v4_py as ecco
Load ecco_grid¶
[5]:
## Set top-level file directory for the ECCO NetCDF files
## =================================================================
## currently set to ~/Downloads/ECCO_V4r4_PODAAC,
## the default if ecco_podaac_download was used to download dataset granules
ECCO_dir = join(user_home_dir,'Downloads','ECCO_V4r4_PODAAC')
[6]:
## Load the model grid
ecco_grid = xr.open_dataset(glob.glob(join(ECCO_dir,'*GEOMETRY*','*.nc'))[0])
Open 2D MONTHLY  snapshots¶
snapshots¶
[7]:
year_start = 1993
year_end = 2017
# open ETAN snapshots (beginning of each month)
ecco_monthly_snaps_etan = (xr.open_mfdataset(join(ECCO_dir,'*SSH*SNAPSHOT*','*-01T*.nc'),\
data_vars='minimal',coords='minimal',compat='override')\
['ETAN']).to_dataset()
ecco_monthly_snaps_obp = xr.open_mfdataset(join(ECCO_dir,'*OBP*SNAPSHOT*','*-01T*.nc'),
data_vars='minimal',coords='minimal',compat='override')
ecco_monthly_snaps = xr.merge((ecco_monthly_snaps_etan,ecco_monthly_snaps_obp))
# time mask for snapshots
time_snap_mask = np.logical_and(ecco_monthly_snaps.time.values >= np.datetime64(str(year_start)+'-01-01','ns'),\
ecco_monthly_snaps.time.values < np.datetime64(str(year_end)+'-01-02','ns'))
ecco_monthly_snaps = ecco_monthly_snaps.isel(time=time_snap_mask)
[8]:
# print time range of monthly snapshots
print(ecco_monthly_snaps.time.isel(time=[0, -1]).values)
['1993-01-01T00:00:00.000000000' '2017-01-01T00:00:00.000000000']
[9]:
# find the record of the last ETAN snapshot
last_record_date = ecco_monthly_snaps.time[-1].values
print(last_record_date)
last_record_year = str(last_record_date)[:4]
2017-01-01T00:00:00.000000000
Open MONTHLY mean data¶
[10]:
## Load ECCO variables
ecco_vars_uvw = xr.open_mfdataset(join(ECCO_dir,'*_OCEAN_3D_VOLUME_FLUX*MONTHLY*','*.nc'),\
data_vars='minimal',coords='minimal',compat='override')
ecco_vars_fflx = xr.open_mfdataset(join(ECCO_dir,'*_FRESH_FLUX*MONTHLY*','*.nc'),\
data_vars='minimal',coords='minimal',compat='override')
ecco_monthly_mean = xr.merge((ecco_vars_uvw,ecco_vars_fflx['oceFWflx']))
# time mask for monthly means
time_mean_mask = np.logical_and(ecco_monthly_mean.time.values >= np.datetime64(str(year_start)+'-01-01','ns'),\
ecco_monthly_mean.time.values < np.datetime64(str(year_end)+'-01-01','ns'))
ecco_monthly_mean = ecco_monthly_mean.isel(time=time_mean_mask)
[11]:
# first and last monthly-mean records
print(ecco_monthly_mean.time.isel(time=[0, -1]).values)
['1993-01-16T12:00:00.000000000' '2016-12-16T12:00:00.000000000']
[12]:
# each monthly mean record is bookended by a snapshot.
# we should have one more snapshot than monthly mean record
print('number of monthly mean records: ', len(ecco_monthly_mean.time))
print('number of monthly snapshot records: ', len(ecco_monthly_snaps.time))
number of monthly mean records: 288
number of monthly snapshot records: 289
Create the xgcm ‘grid’ object¶
the xgcm grid object makes it easy to make flux divergence calculations across different tiles of the lat-lon-cap grid.
[13]:
ecco_xgcm_grid = ecco.get_llc_grid(ecco_grid)
ecco_xgcm_grid
[13]:
<xgcm.Grid>
Y Axis (not periodic, boundary=None):
* center j --> left
* left j_g --> center
Z Axis (not periodic, boundary=None):
* center k --> left
* right k_u --> center
* left k_l --> center
* outer k_p1 --> center
X Axis (not periodic, boundary=None):
* center i --> left
* left i_g --> center
Calculate LHS:  time tendency:
time tendency: 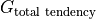 ¶
¶
We calculate the monthly-averaged time tendency of ETAN by differencing monthly ETAN snapshots. Subtract the numpy arrays 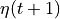 -
- 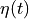 . This operation gives us
. This operation gives us 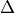
ETAN 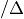 t (month) records.
t (month) records.
[14]:
num_months = len(ecco_monthly_snaps.time)
G_total_tendency_month = \
ecco_monthly_snaps.ETAN.isel(time=range(1,num_months)).values - \
ecco_monthly_snaps.ETAN.isel(time=range(0,num_months-1)).values
# The result is a numpy array of 264 months
print('shape of G_total_tendency_month: ', G_total_tendency_month.shape)
shape of G_total_tendency_month: (288, 13, 90, 90)
[15]:
ecco_monthly_mean.oceFWflx.shape
[15]:
(288, 13, 90, 90)
[16]:
# Convert this numpy array to an xarray Dataarray to take advantage
# of xarray time indexing.
# The easiest way is to copy an existing DataArray that has the
# dimensions and time indexes that we want,
# replace its values, and change its name.
tmp = ecco_monthly_mean.oceFWflx.copy(deep=True)
tmp.values = G_total_tendency_month
tmp.name = 'G_total_tendency_month'
G_total_tendency_month = tmp
# the nice thing is that now the time values of G_total_tendency_month now line
# up with the time values of the time-mean fields (middle of the month)
print('\ntime of first array of G_total_tendency_month');
print(G_total_tendency_month.time[0].values)
time of first array of G_total_tendency_month
1993-01-16T12:00:00.000000000
Now convert 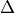
ETAN 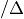 t (month) to
t (month) to 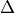
ETAN 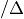 t (seconds) by dividing by the number of seconds in each month.
t (seconds) by dividing by the number of seconds in each month.
[17]:
secs_per_month = (ecco_monthly_snaps.time[1:].values - \
ecco_monthly_snaps.time[0:-1].values).astype('float')/(1.e9) #divide by 1.e9 to convert ns to seconds
# Make a DataArray with the number of seconds in each month,
#time indexed to the times in dETAN_dT_perMonth (middle of each month)
secs_per_month = xr.DataArray(secs_per_month, \
coords={'time': G_total_tendency_month.time.values}, \
dims='time')
# show number of seconds in the first two months:
print('# of seconds in Jan and Feb 1993 ', secs_per_month[0:2].values)
# sanity check: show number of days in the first two months:
print('# of days in Jan and Feb 1993 ', secs_per_month[0:2].values/3600/24)
# of seconds in Jan and Feb 1993 [2678400. 2419200.]
# of days in Jan and Feb 1993 [31. 28.]
[18]:
# convert dETAN_dT_perMonth to perSeconds
G_total_tendency = G_total_tendency_month / secs_per_month
Plot the time-mean 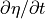 , total
, total 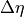 , and one example
, and one example 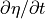 field¶
field¶
Time-mean 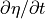 ¶
¶
To calculate the time averaged 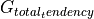 one might be tempted to do the following
one might be tempted to do the following
> G_total_tendency_mean = G_total_tendency.mean('time')
But that would be folly because the ‘mean’ function does not know that the number of days in each month is different! The result would downweight Februarys and upweight Julys. We have to weight the tendency records by the length of each month. A clever way of doing that is provided in the xarray documents: https://xarray-test.readthedocs.io/en/latest/examples/monthly-means.html
In our case we know the length of each month, we just calculated it above in secs_per_month. We will weight each month by the relative # of seconds in each month and sum to get a weighted average.
[19]:
# the weights are just the # of seconds per month divided by total seconds
month_length_weights = secs_per_month / secs_per_month.sum()
The time mean of the ETAN tendency, 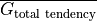 , is given by
, is given by
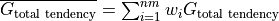
with 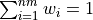 and nm=number of months
and nm=number of months
[20]:
# the weights sum to 1
print(month_length_weights.sum())
<xarray.DataArray ()>
array(1.)
[21]:
# the weighted mean weights by the length of each month (in seconds)
G_total_tendency_mean = (G_total_tendency*month_length_weights).sum('time')
[22]:
plt.figure(figsize=(20,8));
ecco.plot_proj_to_latlon_grid(ecco_grid.XC, ecco_grid.YC,\
G_total_tendency_mean,show_colorbar=True,\
cmin=-1e-9, cmax=1e-9, \
cmap='RdBu_r', user_lon_0=-67,\
dx=map_dx,dy=map_dy);
plt.title('Average $\partial \eta / \partial t$ [m/s]', fontsize=20);
-179.9 112.9
-180.0 113.0
-89.9 89.9
-90.0 90.0
113.10030938622755 179.89970061377244
113.00001 180.0
-89.9 89.9
-90.0 90.0
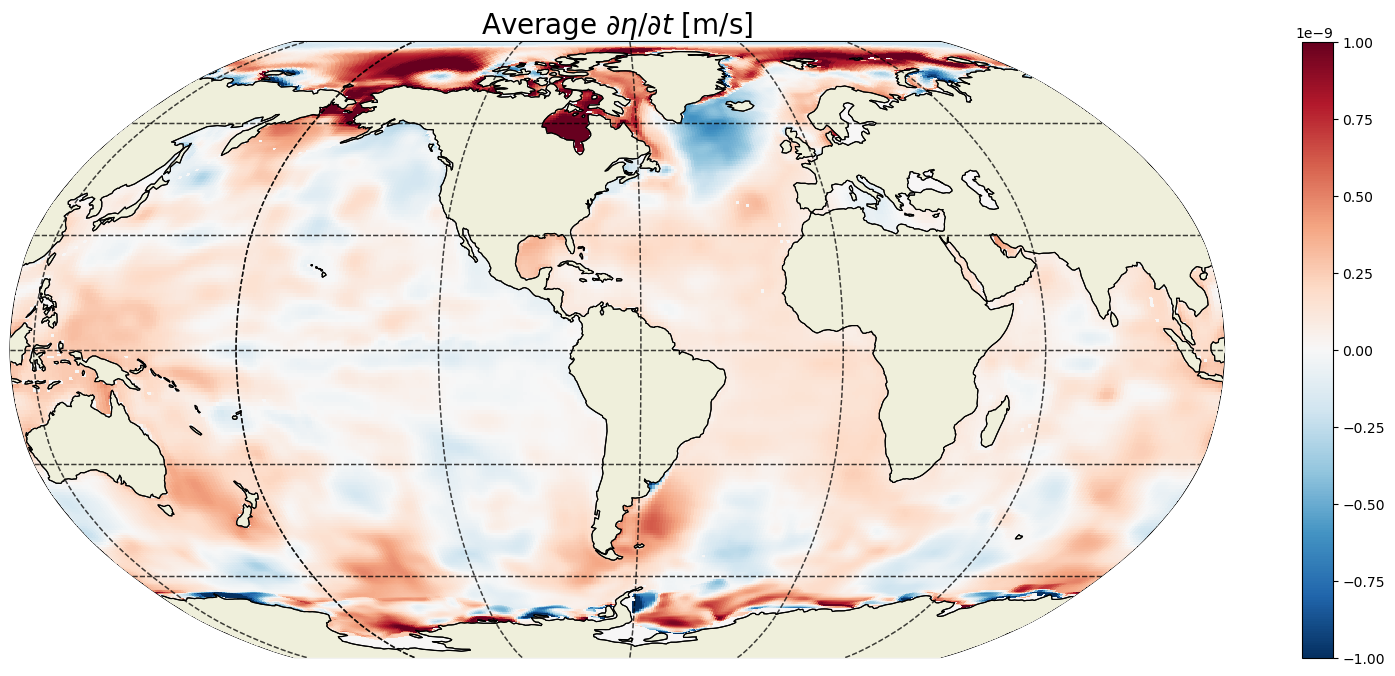
Total 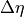 ¶
¶
The time average eta tendency is small, about 1 billionth of a meter per second. The ECCO period is coming up to a billion seconds though… How much did ETAN change over the analysis period?
[23]:
# the number of seconds in the entire period
seconds_in_entire_period = \
float(ecco_monthly_snaps.time[-1] - ecco_monthly_snaps.time[0])/1e9
print ('seconds in analysis period: ', seconds_in_entire_period)
# which is also the sum of the number of seconds in each month
print('sum of seconds in each month ', secs_per_month.sum().values)
seconds in analysis period: 757382400.0
sum of seconds in each month 757382400.0
[24]:
ETAN_delta = G_total_tendency_mean*seconds_in_entire_period
[25]:
plt.figure(figsize=(20,8));
ecco.plot_proj_to_latlon_grid(ecco_grid.XC, ecco_grid.YC, \
ETAN_delta,show_colorbar=True,\
cmin=-1, cmax=1, \
cmap='RdBu_r', user_lon_0=-67, \
dx=map_dx,dy=map_dy);
plt.title('Predicted $\Delta \eta$ [m] from $\partial \eta / \partial t$', \
fontsize=20);
-179.9 112.9
-180.0 113.0
-89.9 89.9
-90.0 90.0
113.10030938622755 179.89970061377244
113.00001 180.0
-89.9 89.9
-90.0 90.0
We can sanity check the total ETAN change that we found by multipling the time-mean ETAN tendency with the number of seconds in the simulation by comparing that with the difference in ETAN between the end of the last month and start of the first month.
[26]:
ETAN_delta_method_2 = ecco_monthly_snaps.ETAN.isel(time=-1).values - \
ecco_monthly_snaps.ETAN.isel(time=0).values
[27]:
plt.figure(figsize=(20,8));
ecco.plot_proj_to_latlon_grid(ecco_grid.XC, ecco_grid.YC, \
ETAN_delta_method_2,
show_colorbar=True,\
cmin=-1, cmax=1, \
cmap='RdBu_r', user_lon_0=-67,\
dx=map_dx,dy=map_dy);
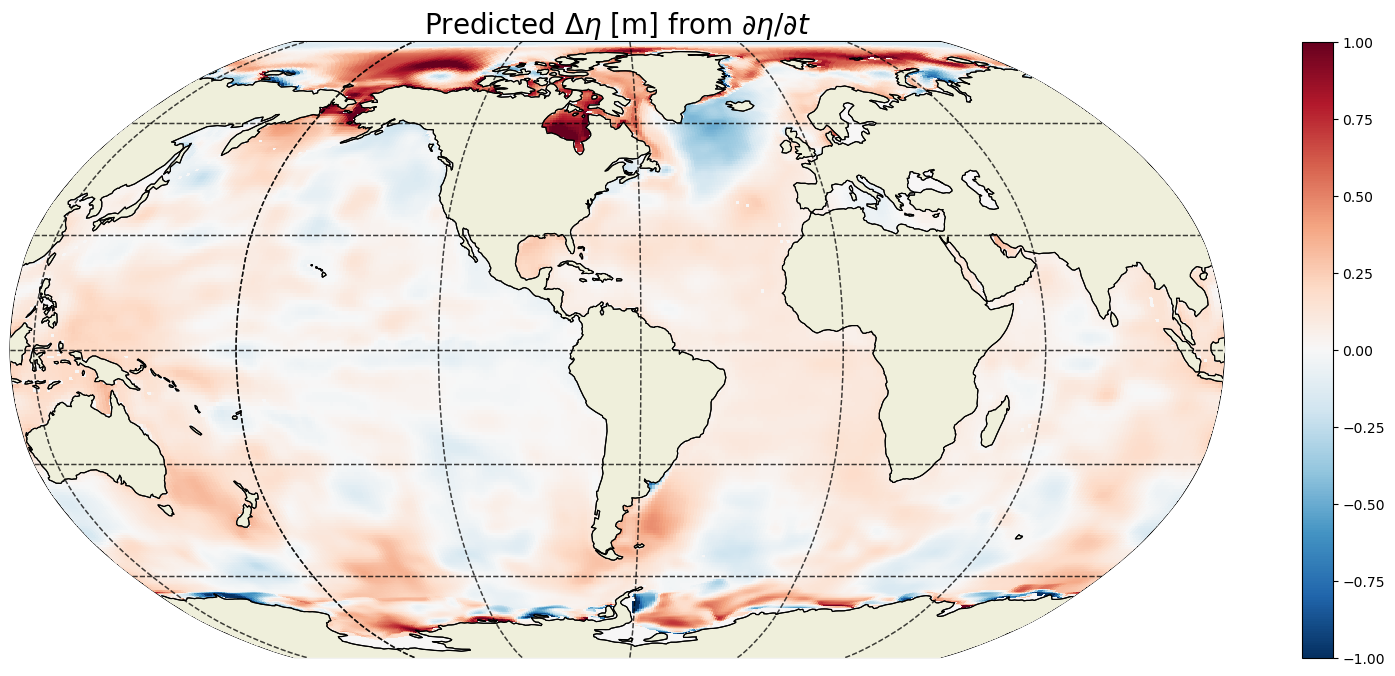
plt.title('Actual $\Delta \eta$ [m]', fontsize=20);
-179.9 112.9
-180.0 113.0
-89.9 89.9
-90.0 90.0
113.10030938622755 179.89970061377244
113.00001 180.0
-89.9 89.9
-90.0 90.0
[28]:
plt.figure(figsize=(20,8));
ecco.plot_proj_to_latlon_grid(ecco_grid.XC, ecco_grid.YC, \
ETAN_delta_method_2-ETAN_delta,\
show_colorbar=True,\
cmin=-1e-6, cmax=1e-6, \
cmap='RdBu_r', user_lon_0=-67,\
dx=map_dx,dy=map_dy);
plt.title('Difference between actual and predicted $\Delta \eta$ [m]', \
fontsize=20);
-179.9 112.9
-180.0 113.0
-89.9 89.9
-90.0 90.0
113.10030938622755 179.89970061377244
113.00001 180.0
-89.9 89.9
-90.0 90.0
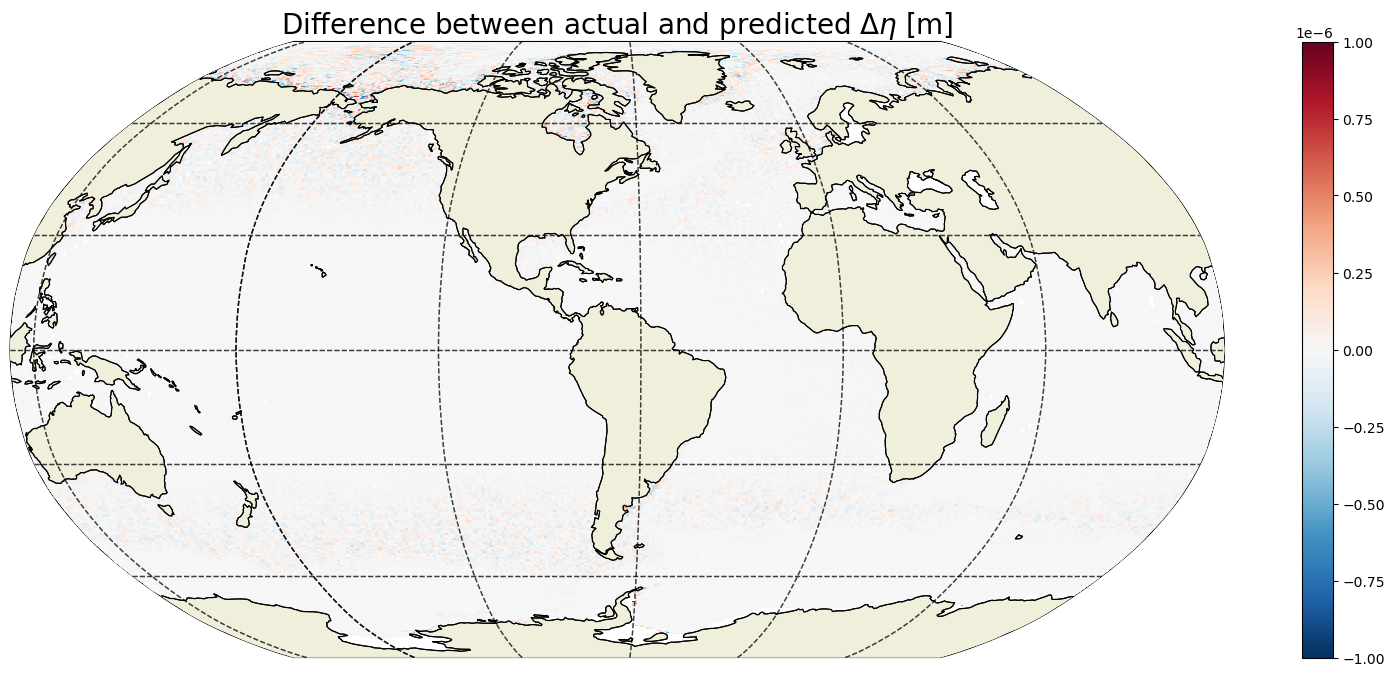
That’s a big woo, these are the same to within 10^-6 meters!
Example 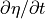 field¶
field¶
[29]:
plt.figure(figsize=(20,8));
curr_t_ind = 100
curr_time = G_total_tendency.time[curr_t_ind].values
print(curr_time)
ecco.plot_proj_to_latlon_grid(ecco_grid.XC, ecco_grid.YC, \
G_total_tendency.isel(time=curr_t_ind),\
show_colorbar=True,\
cmin=-1e-7, cmax=1e-7,\
cmap='RdBu_r', user_lon_0=-67,\
dx=map_dx,dy=map_dy);
plt.title('$\partial \eta / \partial t$ [m/s] during ' +
str(curr_time)[0:4] +'/' + str(curr_time)[5:7], fontsize=20);
2001-05-16T12:00:00.000000000
-179.9 112.9
-180.0 113.0
-89.9 89.9
-90.0 90.0
113.10030938622755 179.89970061377244
113.00001 180.0
-89.9 89.9
-90.0 90.0
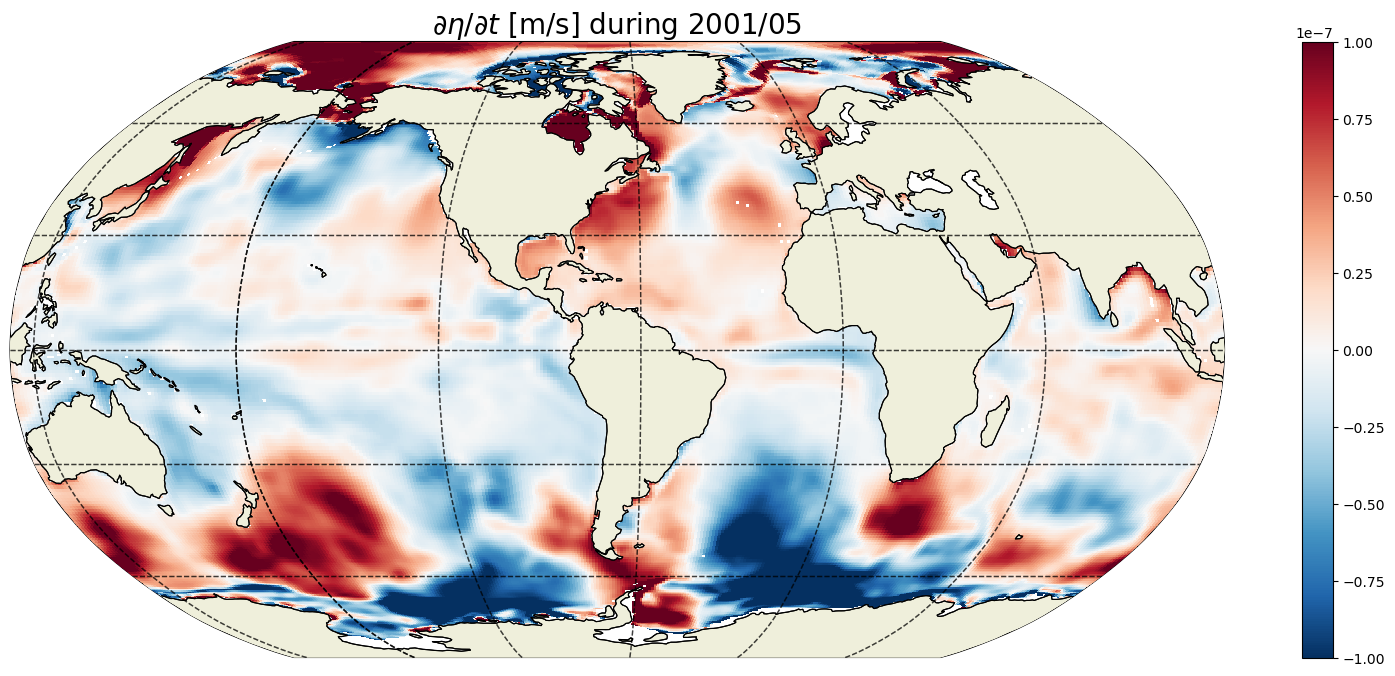
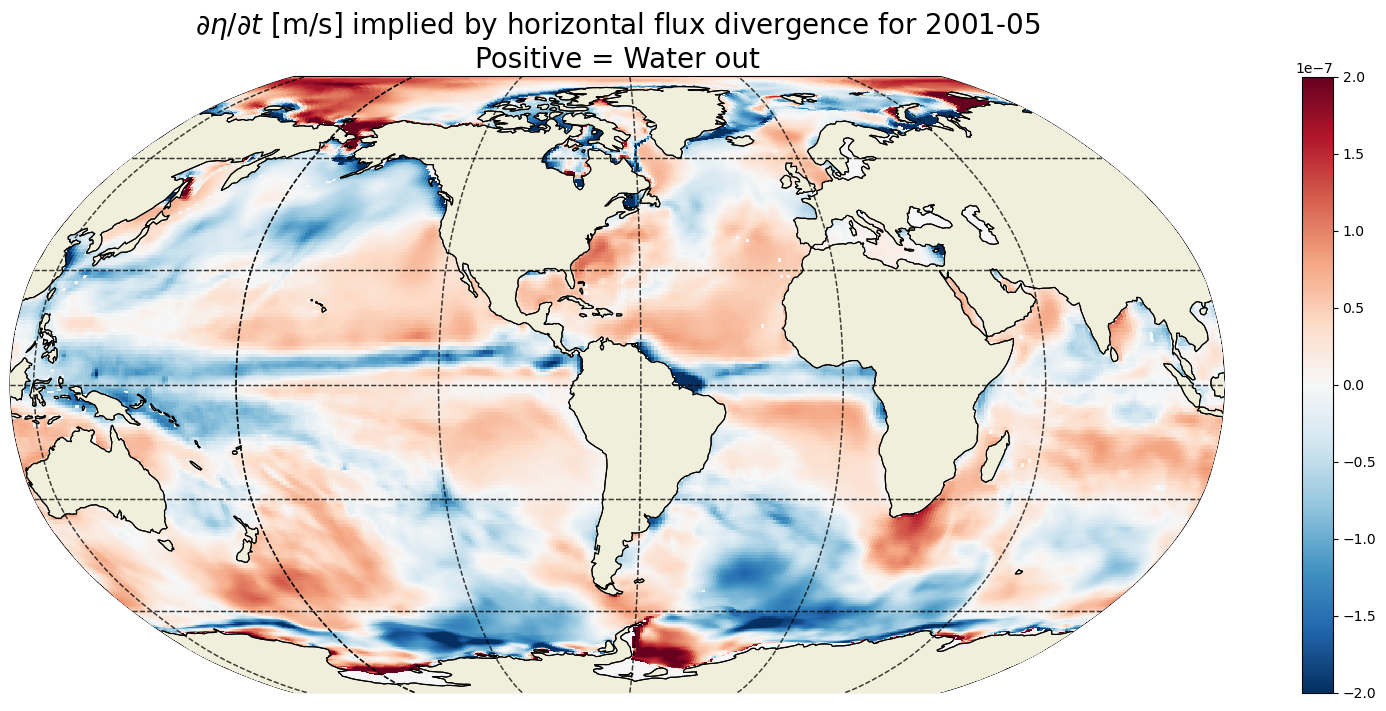
For any given month the time rate of change of ETAN is two orders of magnitude smaller than the 1993-2015 mean. In the above we are looking at May 2001. We see positive ETAN tendency due sea ice melting in the northern hemisphere (e.g., Baffin Bay, Greenland Sea, and Chukchi Sea).
Calculate RHS:  tendency due to surface fluxes,
tendency due to surface fluxes, 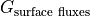 ¶
¶
Surface mass fluxes are given in oceFWflx. Convert surface mass flux to a vertical velocity by dividing by the reference density rhoConst= 1029 kg m-3
[30]:
# tendency of eta implied by surface volume fluxes (m/s)
G_surf_fluxes = ecco_monthly_mean.oceFWflx/rhoconst
Plot the time-mean, total, and one month average of 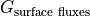 ¶
¶
Time-mean 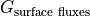 ¶
¶
We calculate the time-mean surface flux  tendency using the same weights as the total
tendency using the same weights as the total  tendency.
tendency.
[31]:
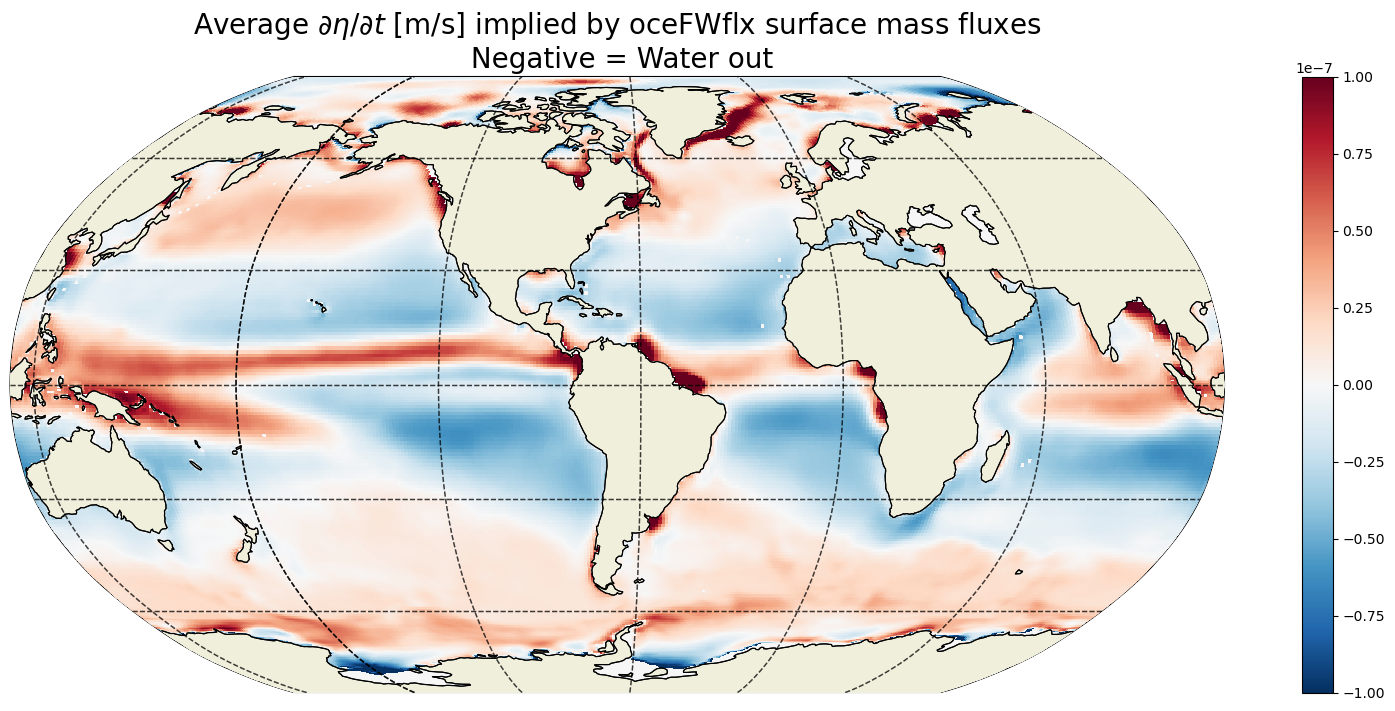
G_surf_fluxes_mean= (G_surf_fluxes*month_length_weights).sum('time')
G_surf_fluxes_mean.shape
[31]:
(13, 90, 90)
[32]:
plt.figure(figsize=(20,8));
ecco.plot_proj_to_latlon_grid(ecco_grid.XC, ecco_grid.YC, \
G_surf_fluxes_mean,
show_colorbar=True,\
cmin=-1e-7, cmax=1e-7, \
cmap='RdBu_r', user_lon_0=-67,
dx=map_dx,dy=map_dy)
plt.title('Average $\partial \eta / \partial t$ [m/s] implied by oceFWflx surface mass fluxes\n Negative = Water out',
fontsize=20);
-179.9 112.9
-180.0 113.0
-89.9 89.9
-90.0 90.0
113.10030938622755 179.89970061377244
113.00001 180.0
-89.9 89.9
-90.0 90.0
Total 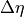 due to surface fluxes¶
due to surface fluxes¶
If there were no other terms on the RHS to balance surface fluxes, the total change in ETAN between 1993 and 2017 would be order of 10s of meters almost everwhere.
[33]:
ETAN_delta_surf_fluxes = G_surf_fluxes_mean*seconds_in_entire_period
[34]:
plt.figure(figsize=(20,8));
ecco.plot_proj_to_latlon_grid(ecco_grid.XC, ecco_grid.YC, \
ETAN_delta_surf_fluxes,show_colorbar=True,\
cmin=-100, cmax=100, \
cmap='RdBu_r', user_lon_0=-67, \
dx=map_dx,dy=map_dy);
plt.title('$\Delta \eta$ [m] implied by oceFWflx surface mass fluxes',
fontsize=20);
-179.9 112.9
-180.0 113.0
-89.9 89.9
-90.0 90.0
113.10030938622755 179.89970061377244
113.00001 180.0
-89.9 89.9
-90.0 90.0
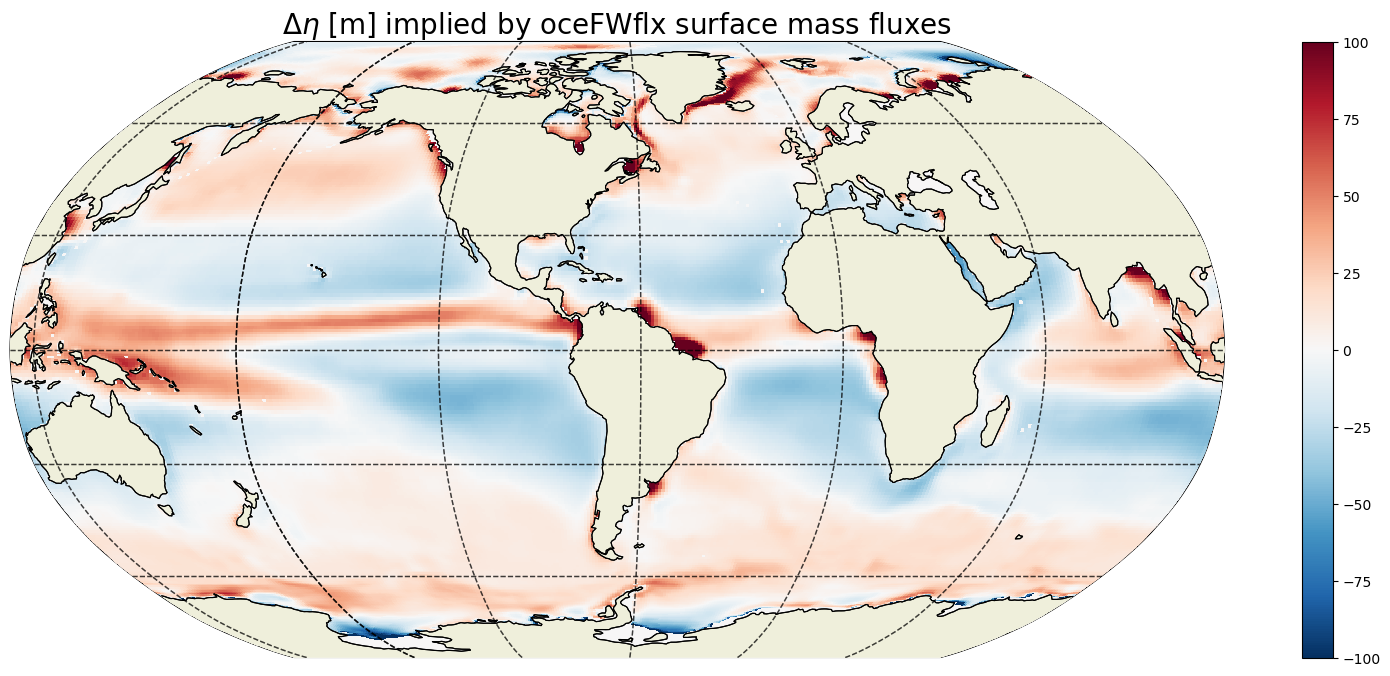
Example  impliedy by surface fluxes¶
impliedy by surface fluxes¶
[35]:
plt.figure(figsize=(20,8));
curr_t_ind = 100
curr_time = G_surf_fluxes.time[curr_t_ind].values
print(curr_time)
ecco.plot_proj_to_latlon_grid(ecco_grid.XC, ecco_grid.YC, \
G_surf_fluxes.isel(time=curr_t_ind),show_colorbar=True,\
cmin=-1e-7, cmax=1e-7, \
cmap='RdBu_r', user_lon_0=-67,\
dx=map_dx,dy=map_dy);
plt.title('$\partial \eta / \partial t$ [m/s] implied by oceFWflx surface mass fluxes ' +
str(curr_time)[0:4] +'-' + str(curr_time)[5:7], fontsize=20);
2001-05-16T12:00:00.000000000
-179.9 112.9
-180.0 113.0
-89.9 89.9
-90.0 90.0
113.10030938622755 179.89970061377244
113.00001 180.0
-89.9 89.9
-90.0 90.0
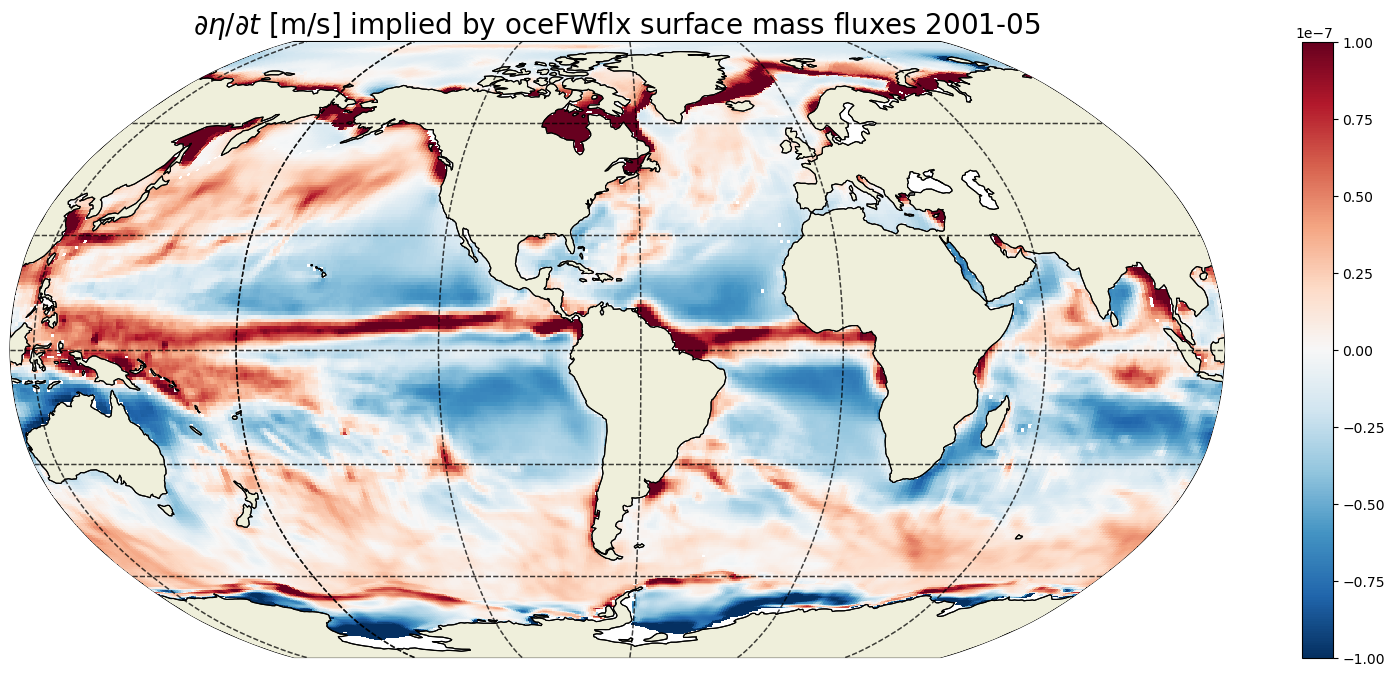
For any given month the time rate of change of ETAN is almost the same as its 22 year mean. Differences are largest in the high latitudes where sea-ice melt and growth during any particular month induce large changes in ETAN.
Calculate RHS:  tendency due to volumetric flux divergence,
tendency due to volumetric flux divergence,  ¶
¶
First we will look at vertical volumetric flux divergence, then horizontal volumetric flux divergence.
Vertical volumetric flux divergence¶
It turns out that WVELMASS at k_l=0 (the top face of the top tracer cell) is proportional to the ocean surface mass flux oceFWflx. The vertical velocity of the ocean surface is equal to the rate at which water is being added or removed across the top surface of the uppermost grid cell. This is demonstrated by differencing the velocity at the top ‘w’ face of the uppermost tracr cell WVELMASS (k_l = 0) and the velocity equivalent of transporting the surface mass flux term oceFWFlx
through this same face.
First, find the time-mean vertical velocity at the liquid ocean surface
[36]:
WVELMASS_surf_mean = \
(ecco_monthly_mean.WVELMASS.isel(k_l=0)*month_length_weights).sum('time')
Next, find the time-mean vertical velocity implied by the oceFWflx at k_l=0:
[37]:
WVEL_from_oceFWflx_mean = \
-(ecco_monthly_mean.oceFWflx*month_length_weights).sum('time')/rhoconst
[38]:
plt.figure(figsize=(15,15))
#plt.sca(axs[0,0])
F=ecco.plot_proj_to_latlon_grid(ecco_grid.XC, ecco_grid.YC, \
WVELMASS_surf_mean,\
show_colorbar=True,\
cmin=-1e-7, cmax=1e-7, \
cmap='RdBu_r', user_lon_0=-67,\
dx=2,dy=2, subplot_grid=[3,1,1]);
F[1].set_title('A: surface velocity from WVEL [m/s]')
F=ecco.plot_proj_to_latlon_grid(ecco_grid.XC, ecco_grid.YC, \
WVEL_from_oceFWflx_mean,\
show_colorbar=True,\
cmin=-1e-7, cmax=1e-7, \
cmap='RdBu_r', user_lon_0=-67,\
dx=2,dy=2, subplot_grid=[3,1,2])
F[1].set_title("B: surface velocity implied by oceFWflx [m/s]")
F=ecco.plot_proj_to_latlon_grid(ecco_grid.XC, ecco_grid.YC, \
WVELMASS_surf_mean-WVEL_from_oceFWflx_mean,\
show_colorbar=True,\
cmin=-1e-7, cmax=1e-7, \
cmap='RdBu_r', user_lon_0=-67,\
dx=2,dy=2, subplot_grid=[3,1,3])
F[1].set_title("difference between A and B");
-178.99657534246575 111.99657534246575
-180.0 113.0
-89.0 89.0
-90.0 90.0
114.01516136363637 178.98484863636364
113.00001 180.0
-89.0 89.0
-90.0 90.0
-178.99657534246575 111.99657534246575
-180.0 113.0
-89.0 89.0
-90.0 90.0
114.01516136363637 178.98484863636364
113.00001 180.0
-89.0 89.0
-90.0 90.0
-178.99657534246575 111.99657534246575
-180.0 113.0
-89.0 89.0
-90.0 90.0
114.01516136363637 178.98484863636364
113.00001 180.0
-89.0 89.0
-90.0 90.0
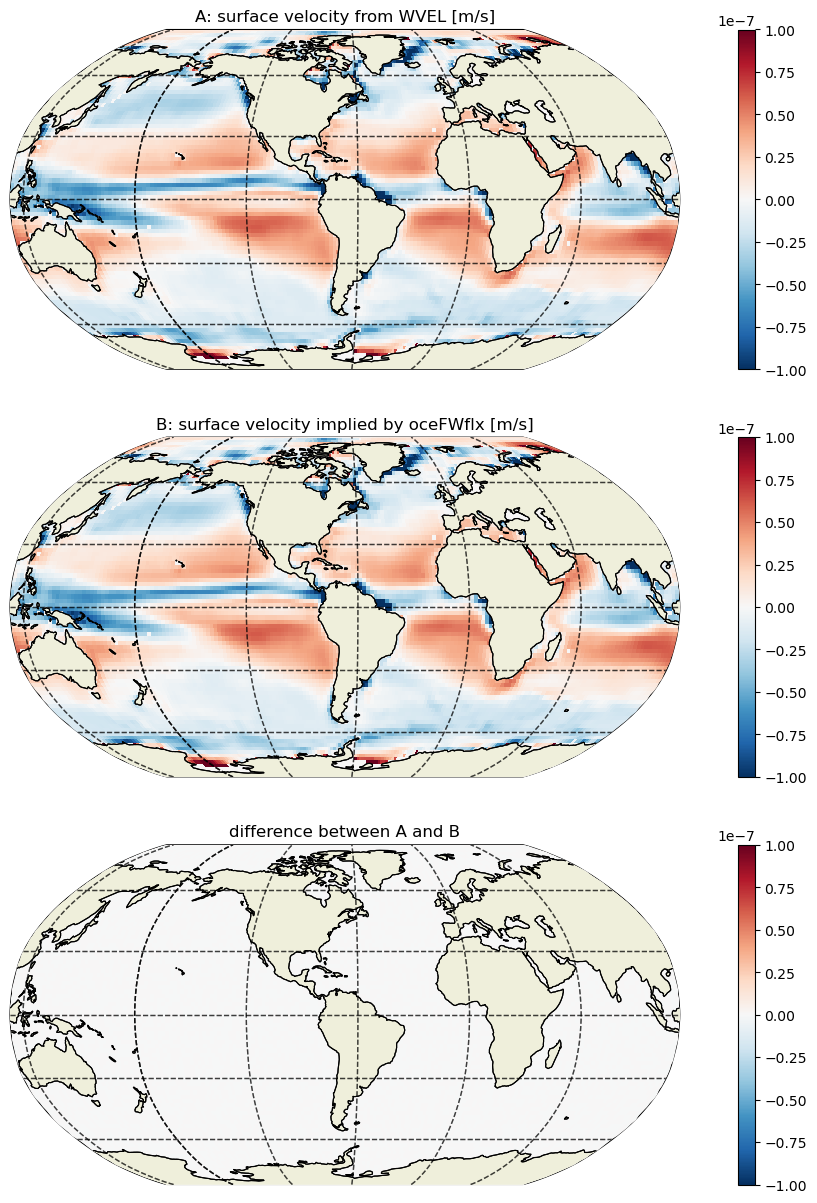
WVELMASS at the surface evidently is the same as the surface velocity implied by the surface mass flux oceFWflx. Thus, we do not actually need oceFWflx to close the volume budget. However, to keep the surface forcing term explicitly represented, we will keep oceFWflx and instead zero out the values of WVELMASS at the surface so as to avoid double counting.
Calculate the vertical volume fluxes at each level: (velocity x grid cell area) [m3 s-1]
[39]:
vol_transport_z = ecco_monthly_mean.WVELMASS * ecco_grid.rA
Set the volume transport at the surface level to be zero because we already counted the fluxes out of the domain with oceFWflx. We will also set the volume transport in land areas (currently NaN values) to zero so the divergence adjacent to the bottom is computed correctly.
[40]:
# vol_transport_z.isel(k_l=0).values[:] = 0
# vol_transport_z.values[ecco_grid.hFacC.values == 0] = 0
# ## For some reason the above commands don't seem to work with dask arrays,
# ## probably due to some complication resetting the values of an existing dask array.
## However, using where works with dask arrays
vol_transport_z = vol_transport_z.where(np.expand_dims(ecco_grid.k_l.values,axis=(0,-1,-2,-3)) != 0,\
0)
vol_transport_z = vol_transport_z.where(ecco_grid.hFacC.values > 0,0)
Each grid cell has a top and bottom surface and therefore WVELMASSshould have 51 vertical levels (one more than the number of tracer cells). For some reason we only have 50 vertical levels, with the bottom of the 50th tracer cell missing. To calculate vertical flux divergence we need to add this 51st WVELMASS which is everywhere zero (no volume flux from the seafloor). The xgcm library handles this in its diff routine by specifying the boundary=’fill’ and fill_value = 0.
[41]:
# volume flux divergence into each grid cell, m^3 / s
vol_vert_divergence = ecco_xgcm_grid.diff(vol_transport_z, 'Z', \
boundary='fill', fill_value=0)
# change in eta per unit time due to volumetric vertical convergence
# at each depth level: m/s
G_vertical_flux_divergence = vol_vert_divergence / ecco_grid.rA;
[42]:
# change in eta per unit time due to vertical integral of
# volumetric horizonal convergence: m/s
G_vertical_flux_divergence_depth_integrated = G_vertical_flux_divergence.sum('k')
[43]:
# Calculate the time-mean surface flux $\eta$ tendency using
# the same weights as the total $\eta$ tendency.
G_vertical_flux_divergence_depth_integrated_time_mean = \
(G_vertical_flux_divergence_depth_integrated * month_length_weights).sum('time')
Plot the time-mean 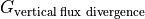 ¶
¶
[44]:
plt.figure(figsize=(20,8));
ecco.plot_proj_to_latlon_grid(ecco_grid.XC, ecco_grid.YC,\
G_vertical_flux_divergence_depth_integrated_time_mean,\
show_colorbar=True,\
cmap='RdBu_r', \
cmin=-1e-9, cmax=1e-9,
dx=map_dx,dy=map_dy);
plt.title('Average $\partial \eta / \partial t$ [m/s] due to vertical flux divergence\n Negative = Water out',
fontsize=20);
-179.9 179.9
-180.0 180.0
-89.9 89.9
-90.0 90.0
These values are everywhere essentially zero (numerical noise). On average, the only vertical flux divergence in the column is across the ocean surface. Below the surface, the sum of vertical flux divergence in all tracer cells in the column must be zero because any divergence in any one particular cell is exactly offset by convergence in another cell. Net convergence into the column manifests as a positive vertical velocity at the surface which is equal to oceFWflux in the time-mean. Thanks to Hong Zhang for comments that improved this explanation
Horizontal Volume Flux Divergence¶
Note: when using at least one recent version of
xgcm(v0.8.1), errors were triggered when callingdiff_2d_vectorbelow. If you have this issue, as a temporary fix you can locate thexgcmdirectoryimport xgcm print(xgcm.__path__)and then substitute
padding.pyandgrid_ufunc.pywith the files linked below:Alternatively, you can revert
xgcmto an earlier version (e.g., v0.6.0) that should not have this issue.
[45]:
# Volumetric transports in x and y(m^3/s)
vol_transport_x = ecco_monthly_mean.UVELMASS * ecco_grid.dyG * ecco_grid.drF
vol_transport_y = ecco_monthly_mean.VVELMASS * ecco_grid.dxG * ecco_grid.drF
[46]:
# Set fluxes on land to zero (instead of NaN)
vol_transport_x = vol_transport_x.where(ecco_grid.hFacW.values > 0,0)
vol_transport_y = vol_transport_y.where(ecco_grid.hFacS.values > 0,0)
# Difference of horizontal transports in x and y directions
vol_flux_diff = ecco_xgcm_grid.diff_2d_vector({'X': vol_transport_x, \
'Y': vol_transport_y},\
boundary='fill')
# volume flux divergence into each grid cell, m^3 / s
vol_horiz_divergence = (vol_flux_diff['X'] + vol_flux_diff['Y'])
# restore time coordinate to DataArray (lost in xgcm.diff_2d_vector operation)
vol_horiz_divergence = vol_horiz_divergence.assign_coords({'time':vol_transport_x.time.data})
# change in eta per unit time due to volumetric horizonal
# convergence at each depth level: m/s
# a positive DIVERGENCE leads to negative eta tendency
G_vol_horiz_divergence = -vol_horiz_divergence / ecco_grid.rA
# change in eta in each grid cell per unit time due to horiz. divergence: m/s
G_vol_horiz_divergence_depth_integrated = G_vol_horiz_divergence.sum('k').compute()
[47]:
# calculate time-mean using the month length weights
G_vol_horiz_divergence_depth_integrated_mean = \
(G_vol_horiz_divergence_depth_integrated * month_length_weights).sum('time')
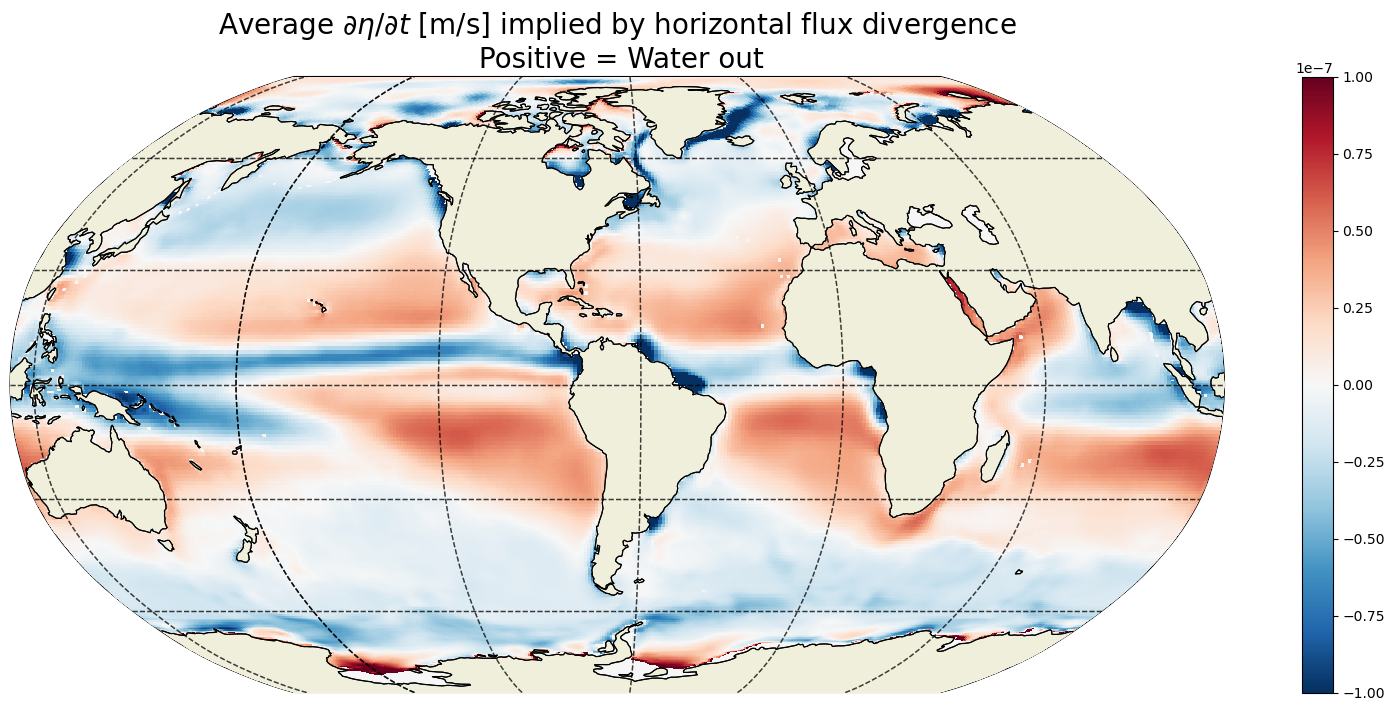
Plot the time-mean 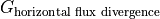 ¶
¶
[48]:
plt.figure(figsize=(20,8));
obj = ecco.plot_proj_to_latlon_grid(ecco_grid.XC, ecco_grid.YC, \
G_vol_horiz_divergence_depth_integrated_mean,\
show_colorbar=True,\
cmin=-1e-7, cmax=1e-7, \
cmap='RdBu_r', user_lon_0=-67,\
dx=map_dx,dy=map_dy);
plt.title('Average $\partial \eta / \partial t$ [m/s] implied by horizontal flux divergence\n Positive = Water out',
fontsize=20);
-179.9 112.9
-180.0 113.0
-89.9 89.9
-90.0 90.0
113.10030938622755 179.89970061377244
113.00001 180.0
-89.9 89.9
-90.0 90.0
Plot one example 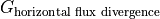 ¶
¶
[49]:
curr_t_ind = 100
curr_time = ecco_monthly_mean.time.values[curr_t_ind]
curr_timestr = str(curr_time)[0:4]+'-'+str(curr_time)[5:7]
plt.figure(figsize=(20,8));
ecco.plot_proj_to_latlon_grid(ecco_grid.XC, ecco_grid.YC, \
G_vol_horiz_divergence_depth_integrated.isel(time=100),
show_colorbar=True,\
cmin=-2e-7, cmax=2e-7, \
cmap='RdBu_r', user_lon_0=-67,\
dx=map_dx,dy=map_dy);
plt.title('$\partial \eta / \partial t$ [m/s] implied by horizontal flux divergence for '\
+curr_timestr+'\nPositive = Water out',
fontsize=20);
-179.9 112.9
-180.0 113.0
-89.9 89.9
-90.0 90.0
113.10030938622755 179.89970061377244
113.00001 180.0
-89.9 89.9
-90.0 90.0
Plot 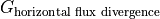 at 100m depth¶
at 100m depth¶
[50]:
plt.figure(figsize=(20,8));
ecco.plot_proj_to_latlon_grid(ecco_grid.XC, ecco_grid.YC, \
G_vol_horiz_divergence.isel(k=10,time=100),
show_colorbar=True,\
cmin=-2e-6, cmax=2e-6, \
cmap='RdBu_r', user_lon_0=-67,\
dx=map_dx,dy=map_dy);
plt.title('$\partial \eta / \partial t$ [m/s] at 100 m implied by horizontal flux divergence for '\
+curr_timestr+'\nPositive = Water out',
fontsize=20);
-179.9 112.9
-180.0 113.0
-89.9 89.9
-90.0 90.0
113.10030938622755 179.89970061377244
113.00001 180.0
-89.9 89.9
-90.0 90.0

Comparison of LHS and RHS¶
Time mean difference of LHR and RHS¶
Plot the time-mean difference between the LHS and RHS of the volume budget equation.
[51]:
#LHS ETA TENDENCY
a = G_total_tendency_mean
# RHS ETA TENDENCY FROM VOL DIVERGENCE AND SURFACE FLUXES
b = G_vol_horiz_divergence_depth_integrated_mean
c = G_surf_fluxes_mean
delta = a - b -c
[52]:
plt.figure(figsize=(20,8));
ecco.plot_proj_to_latlon_grid(ecco_grid.XC, ecco_grid.YC, delta, \
show_colorbar=True,\
cmin=-1e-9, cmax=1e-9, \
cmap='RdBu_r', \
dx=map_dx,dy=map_dy);
plt.title('Residual $\partial \eta / \partial t$ [m/s]: LHS - RHS ',
fontsize=20);
-179.9 179.9
-180.0 180.0
-89.9 89.9
-90.0 90.0
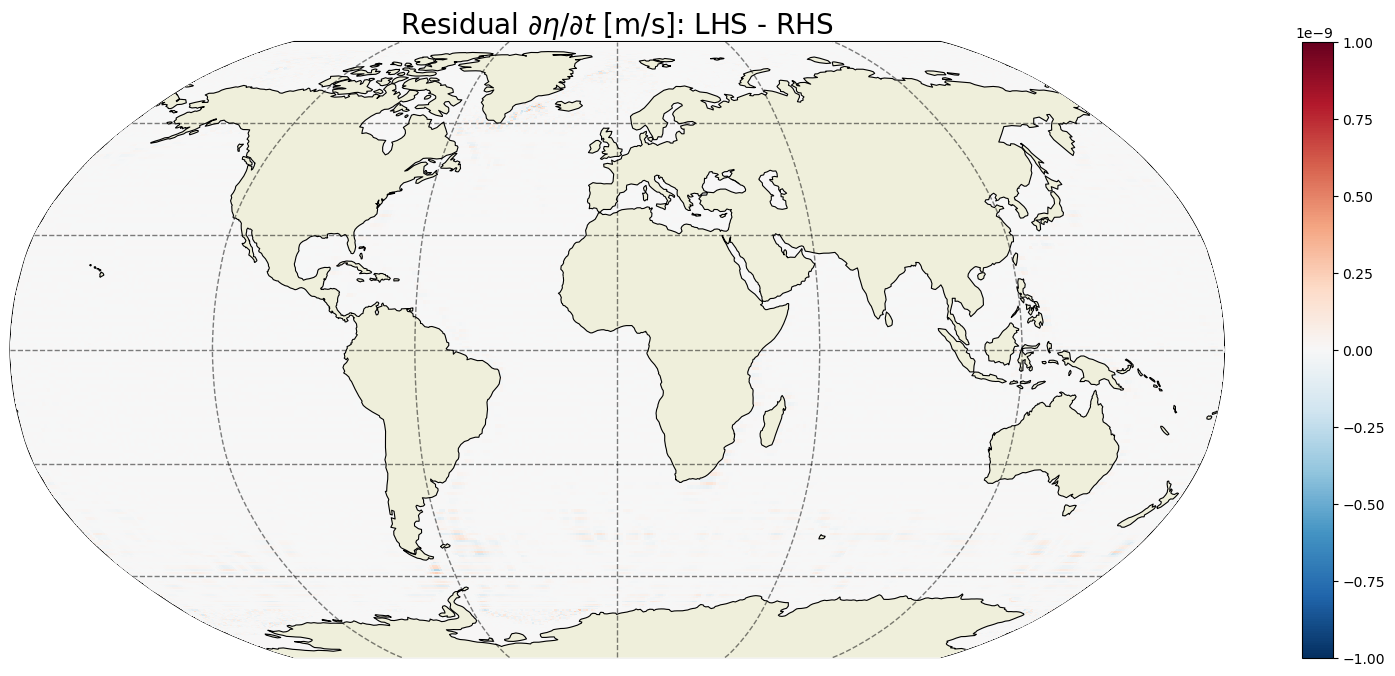
The residual of the time-mean surface velocity tendency terms is essentially zero. We can look at the distribution of residuals to get a little more confidence.
Histogram of residuals¶
[53]:
tmp = np.abs( a-b-c).values.ravel();
plt.figure(figsize=(10,3));
plt.hist(tmp[np.nonzero(tmp > 0)],np.linspace(0, .5e-10,1000));
plt.grid()
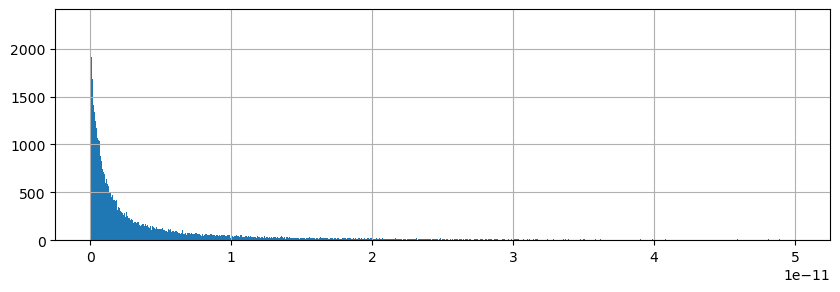
Almost all residuals < 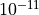 m/s. We can close the ETAN budget using UVELMASS, VVELMASS,
m/s. We can close the ETAN budget using UVELMASS, VVELMASS, WVELMASS and oceFWflx.
Note: As stated earlier, we don’t actually need
oceFWflxbecause the surface velocity ofWVELMASSis proportional tooceFWflxbut we kept it so that the surface forcing term is explicit.
ETAN budget closure through time¶
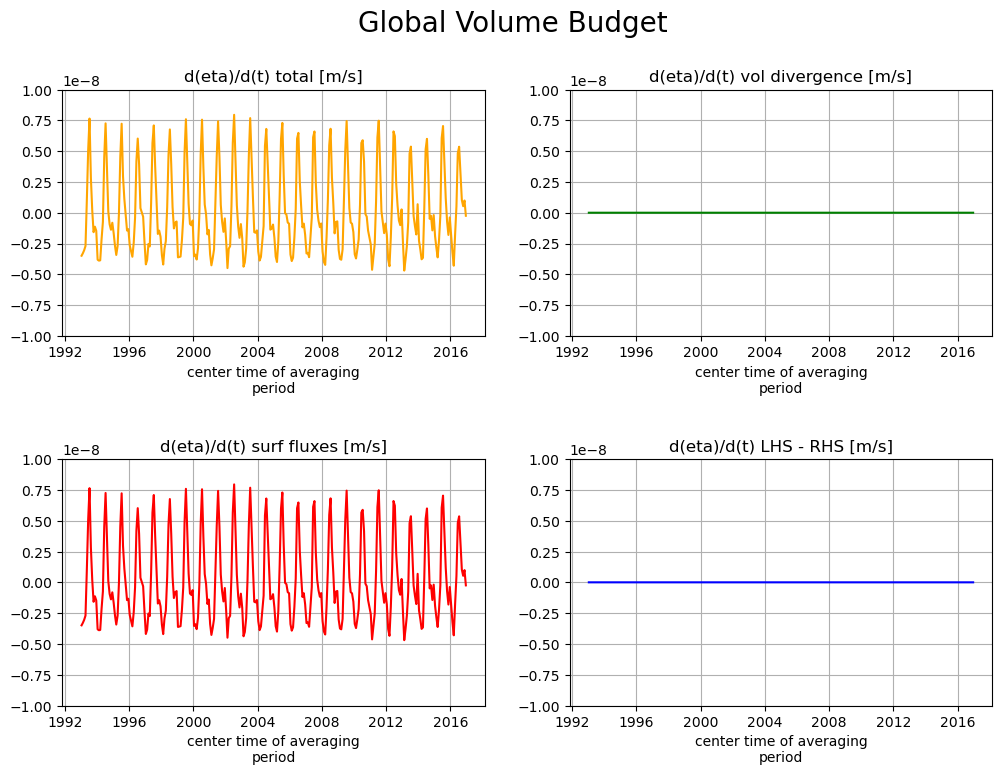
Global average ETAN budget closure¶
Another way of demonstrating volume budget closure is to show the global spatially-averaged ETAN tendency terms through time
[54]:
# LHR and RHS through time
a = G_total_tendency
b = G_vol_horiz_divergence_depth_integrated
c = G_surf_fluxes
# residuals
d = a-b-c
area_masked = ecco_grid.rA.where(ecco_grid.hFacC.isel(k=0) > 0)
# take area-weighted mean of these terms
tmp_a=(a*area_masked).sum(dim=('i','j','tile'))/area_masked.sum()
tmp_b=(b*area_masked).sum(dim=('i','j','tile'))/area_masked.sum()
tmp_c=(c*area_masked).sum(dim=('i','j','tile'))/area_masked.sum()
tmp_d=(d*area_masked).sum(dim=('i','j','tile'))/area_masked.sum()
# result is four time series
tmp_a.dims
[54]:
('time',)
[55]:
fig, axs = plt.subplots(2, 2, figsize=(12,8))
plt.sca(axs[0,0])
tmp_a.plot(color='orange')
axs[0,0].set_title("d(eta)/d(t) total [m/s]")
plt.grid()
plt.ylim([-1e-8, 1e-8]);
plt.sca(axs[0,1])
tmp_b.plot(color='g')
axs[0,1].set_title("d(eta)/d(t) vol divergence [m/s]")
plt.grid()
plt.ylim([-1e-8, 1e-8]);
plt.sca(axs[1,0])
tmp_c.plot(color='r')
axs[1,0].set_title("d(eta)/d(t) surf fluxes [m/s]")
plt.grid()
plt.ylim([-1e-8, 1e-8]);
plt.sca(axs[1,1])
tmp_d.plot(color='b')
axs[1,1].set_title("d(eta)/d(t) LHS - RHS [m/s]")
plt.grid()
plt.subplots_adjust(hspace = .5, wspace=.2)
plt.ylim([-1e-8, 1e-8])
plt.suptitle('Global Volume Budget',fontsize=20);
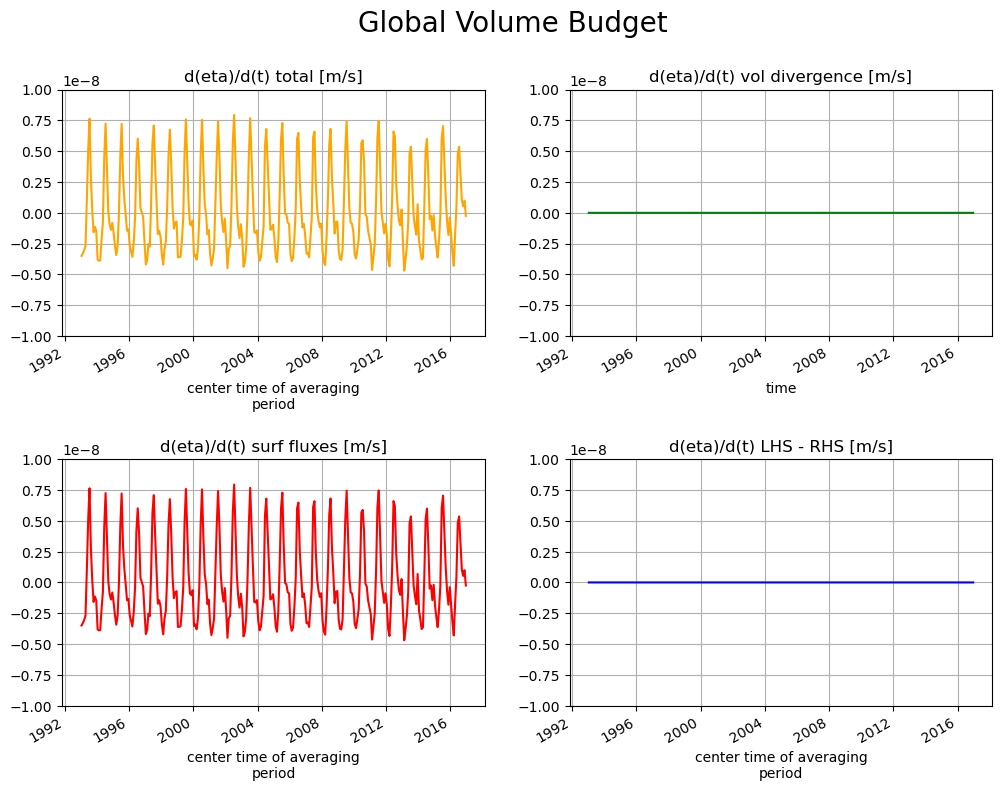
When averaged over the entire ocean surface the volumetric divergence has no net impact on 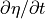 . This makes sence because horizontal flux divergence can only redistributes volume. Globally,
. This makes sence because horizontal flux divergence can only redistributes volume. Globally,  can only change via net surface fluxes.
can only change via net surface fluxes.
Local ETAN budget closure¶
Locally we expect that volume divergence can impact  . This is demonstrated for a single point the Arctic.
. This is demonstrated for a single point the Arctic.
[56]:
# Recall, from above...
#a = G_total_tendency
#b = G_vol_horiz_divergence_depth_integrated
#c = G_surf_fluxes
#d = a-b-c
tmp_aa = a.isel(tile=6,j=40,i=29)
tmp_bb = b.isel(tile=6,j=40,i=29)
tmp_cc = c.isel(tile=6,j=40,i=29)
tmp_dd = d.isel(tile=6,j=40,i=29)
fig, axs = plt.subplots(2, 2, figsize=(12,8))
plt.sca(axs[0,0])
tmp_aa.plot(color='orange')
axs[0,0].set_title("d(eta)/d(t) total [m/s]")
plt.ticklabel_format(axis='y', style='sci', useMathText=True)
plt.ylim([-5e-7, 5e-7]);
plt.grid()
plt.sca(axs[0,1])
tmp_bb.plot(color='g')
axs[0,1].set_title("d(eta)/d(t) vol divergence [m/s]")
plt.ticklabel_format(axis='y', style='sci', useMathText=True)
plt.ylim([-5e-7, 5e-7]);
plt.grid()
plt.sca(axs[1,0])
tmp_cc.plot(color='r')
axs[1,0].set_title("d(eta)/d(t) surf fluxes [m/s]")
plt.ticklabel_format(axis='y', style='sci', useMathText=True)
plt.ylim([-5e-7, 5e-7]);
plt.grid()
plt.sca(axs[1,1])
tmp_dd.plot(color='b')
axs[1,1].set_title("d(eta)/d(t) LHS - RHS [m/s]")
plt.ticklabel_format(axis='y', style='sci', useMathText=True)
plt.ylim([-5e-7, 5e-7]);
plt.grid()
plt.subplots_adjust(hspace = .5, wspace=.2)
plt.suptitle('Volume Budget for one Arctic Ocean point',
fontsize=20);
Indeed, the volume divergence term does contribute to  variations at this one point.
variations at this one point.
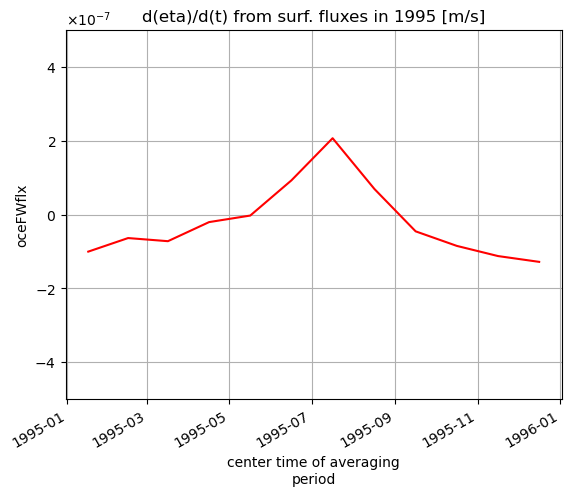
The seasonal cycle of surface fluxes from sea-ice growth and melt can be seen in the surface fluxes term (plotted below for just the year 1995)
[57]:
tmp_cc.sel(time='1995').plot(color='r')
plt.ticklabel_format(axis='y', style='sci', useMathText=True)
plt.ylim([-5e-7, 5e-7]);
plt.grid()
plt.title('d(eta)/d(t) from surf. fluxes in 1995 [m/s]');
Predicted vs. actual  ¶
¶
As we have shown, in our Boussinesq model the only term that can change global mean model sea level anomaly  is net surface freshwater flux. Let us compare the time-evolution of
is net surface freshwater flux. Let us compare the time-evolution of  implied by surface freshwater fluxes and the actual
implied by surface freshwater fluxes and the actual  from the model output.
from the model output.
 time series is calculated by time integrating :math:`G_{surface fluxes}`.
time series is calculated by time integrating :math:`G_{surface fluxes}`. time series anomaly relative to the
time series anomaly relative to the 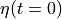 .
.[58]:
area_masked = ecco_grid.rA.where(ecco_grid.maskC.isel(k=0) == 1)
dETA_per_month_predicted_from_surf_fluxes = \
((G_surf_fluxes * area_masked).sum(dim=('i','j','tile')) / \
area_masked.sum())*secs_per_month
ETA_predicted_by_surf_fluxes = \
np.cumsum(dETA_per_month_predicted_from_surf_fluxes.values)
ETA_from_ETAN = \
(ecco_monthly_snaps.ETAN * area_masked).sum(dim=('i','j','tile')) / \
area_masked.sum().compute()
# plotting
plt.figure(figsize=(14,5));
plt.plot(dETA_per_month_predicted_from_surf_fluxes.time, \
ETA_predicted_by_surf_fluxes,'b.')
plt.plot(ETA_from_ETAN.time.values, ETA_from_ETAN-ETA_from_ETAN.values[0],'r-')
plt.grid()
plt.ylabel('global mean $\eta$');
plt.legend(('predicted', 'actual'));
plt.title('$\eta(t)$ as predicted from net surface fluxes and model ETAN [m]',
fontsize=20);
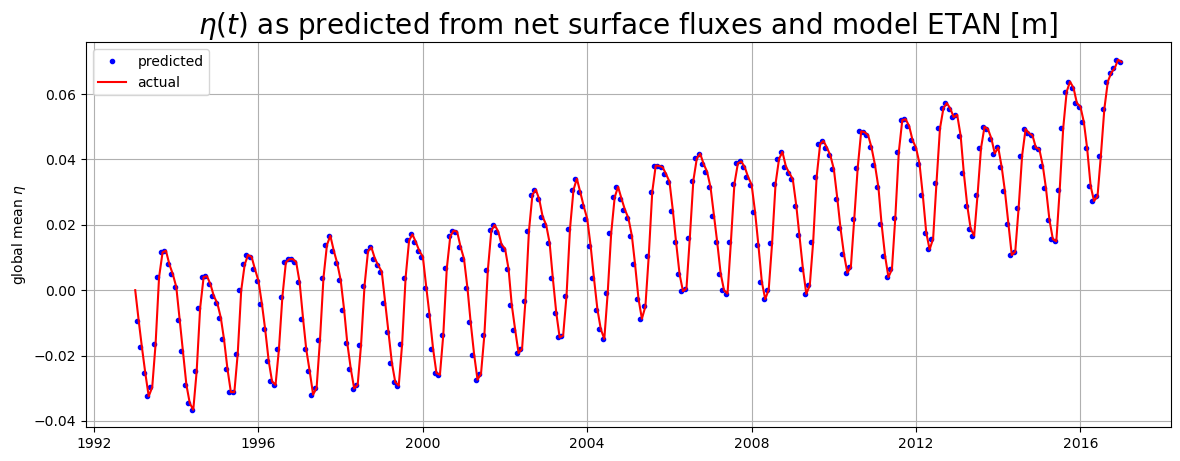
The first predicted  occurs at the end of the first month (one month time integral of
occurs at the end of the first month (one month time integral of 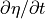 ). The first actual
). The first actual  is set to be zero.
is set to be zero.
The above plot is another way of confirming that in our Boussinesq model the only term that can change global mean model sea level anomaly  is net surface freshwater flux. To account for changes in global mean density we must apply the Greatbatch correction, inverse-barometer correction, and a correction term to account for the fact that sea-ice does not ‘float’ on top of the ocean but in fact displaces seawater upwards. All of these corrections are made for the term
is net surface freshwater flux. To account for changes in global mean density we must apply the Greatbatch correction, inverse-barometer correction, and a correction term to account for the fact that sea-ice does not ‘float’ on top of the ocean but in fact displaces seawater upwards. All of these corrections are made for the term SSH, dynamic
sea surface height anomaly (not shown here).
One can compare the sea level rise from mass fluxes in ECCO vs those estimated from GRACE and other datasets published by the WCRP Global Sea Level Budget Group: Global sea-level budget 1993-present, Earth Syst. Sci. Data, 10, 1551-1590, https://doi.org/10.5194/essd-10-1551-2018, 2018.
Available here. See Figure 16. https://www.earth-syst-sci-data.net/10/1551/2018/essd-10-1551-2018.pdf
[59]:
# Annual mean SL calculation must account for different lengths of each month.
# step 1. weight predicted eta by seconds in each month
tmp1=ETA_predicted_by_surf_fluxes*secs_per_month
# step 2, group records by year and sum across each year
tmp2=tmp1.groupby('time.year').sum()
# step 3, group secs per month by year and sum across each year
secs_per_year = secs_per_month.groupby('time.year').sum()
# step 3, divide time-weighted ETA by seconds per year
annual_mean_GMSL_due_to_mass_fluxes =tmp2/secs_per_year
num_years = len(annual_mean_GMSL_due_to_mass_fluxes.year.values)
plt.figure(figsize=(8,5));
# the -0.13 is to make the starting value comparable with WCRP fig 16.
plt.bar(annual_mean_GMSL_due_to_mass_fluxes.year.values[12:num_years],\
1000*(annual_mean_GMSL_due_to_mass_fluxes.values[12:num_years]-.017), \
color='k')
plt.grid()
plt.xticks(np.arange(2005,
annual_mean_GMSL_due_to_mass_fluxes.year.values[-1]+1,step=1));
plt.title('Sea level (mm) caused by mass fluxes');
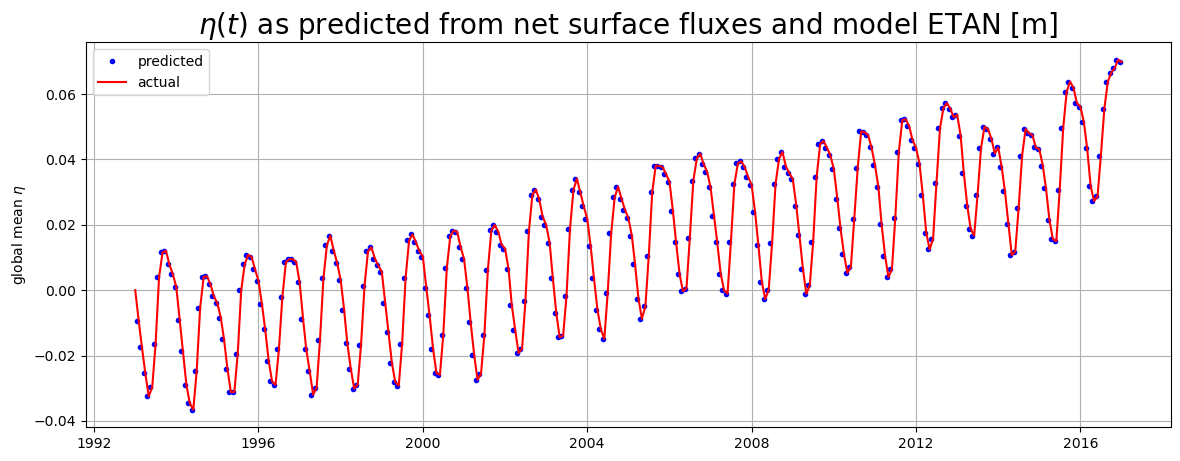
vs the WCRP data:
[60]:
from IPython.display import Image
Image('../figures/cazenave_ocean_mass.png')
[60]:
Time-mean  due to net freshwater fluxes¶
due to net freshwater fluxes¶
We can easily calculate the time mean rate of global sea level rise due to net freshwater flux.
[61]:
x=(G_surf_fluxes_mean * area_masked).sum() / area_masked.sum()
total_GMSLR_due_to_mass_fluxes = x*seconds_in_entire_period
print('total global mean sea level rise due to mass fluxes m: ', \
total_GMSLR_due_to_mass_fluxes.values)
total global mean sea level rise due to mass fluxes m: 0.06982078709392565
Dividing this by the total number of years in the analysis period gives a average rate per year:
[62]:
total_number_of_years = len(secs_per_month)/12
total_number_of_years
[62]:
24.0
[63]:
mean_rate_of_GMSLR_due_to_mass_fluxes = \
total_GMSLR_due_to_mass_fluxes/total_number_of_years
print('mean rate of GMSLR due to mass fluxes [mm/yr] ', \
1000*mean_rate_of_GMSLR_due_to_mass_fluxes.values)
mean rate of GMSLR due to mass fluxes [mm/yr] 2.909199462246902
Compare with other estimates of GMSLR due to mass fluxes.